Research
Overview
My research bridges computational mathematics, machine learning, and scientific computing to advance learning-augmented scientific discovery. Rather than treating learning as a black-box surrogate, I embed it directly within numerical algorithms to accelerate and stabilize many-solve workflows. Achieving accuracy, convergence, and scalability requires end-to-end co-design, integrating structure-aware models, geometry-aware optimization, and hardware-efficient computation into unified solvers.
Research Directions
Models: Structure-Aware Representations
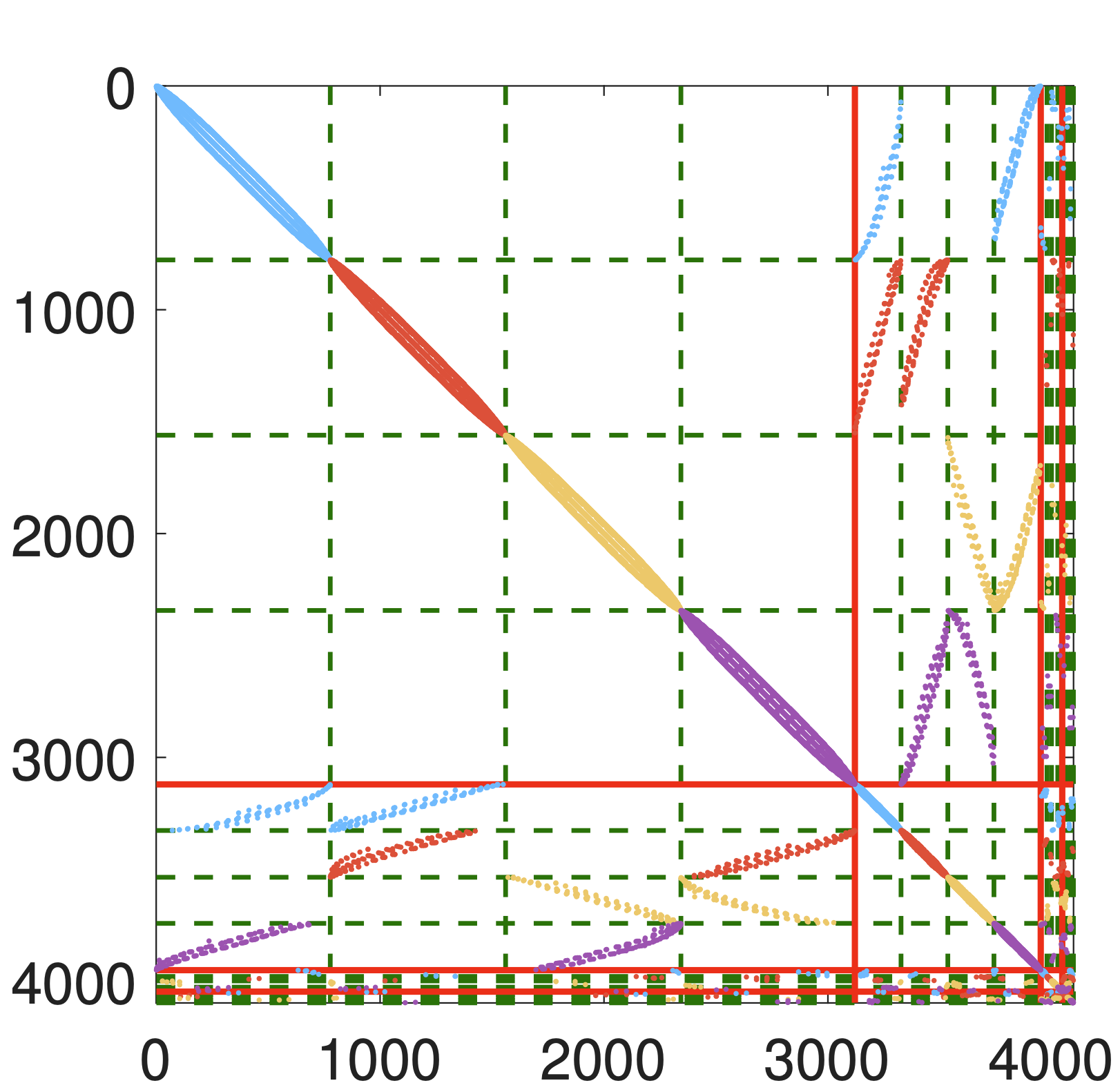
From a numerical perspective, representation power alone is insufficient; models must define an approximation space compatible with underlying physical operators. I design physics- and structure-aware architectures such as multiscale networks for Green's functions and line-graph models that explicitly capture locality and sparsity, ensuring parameter efficiency and reliable generalization across varying regimes.
Optimization: Geometry-Aware Convergence
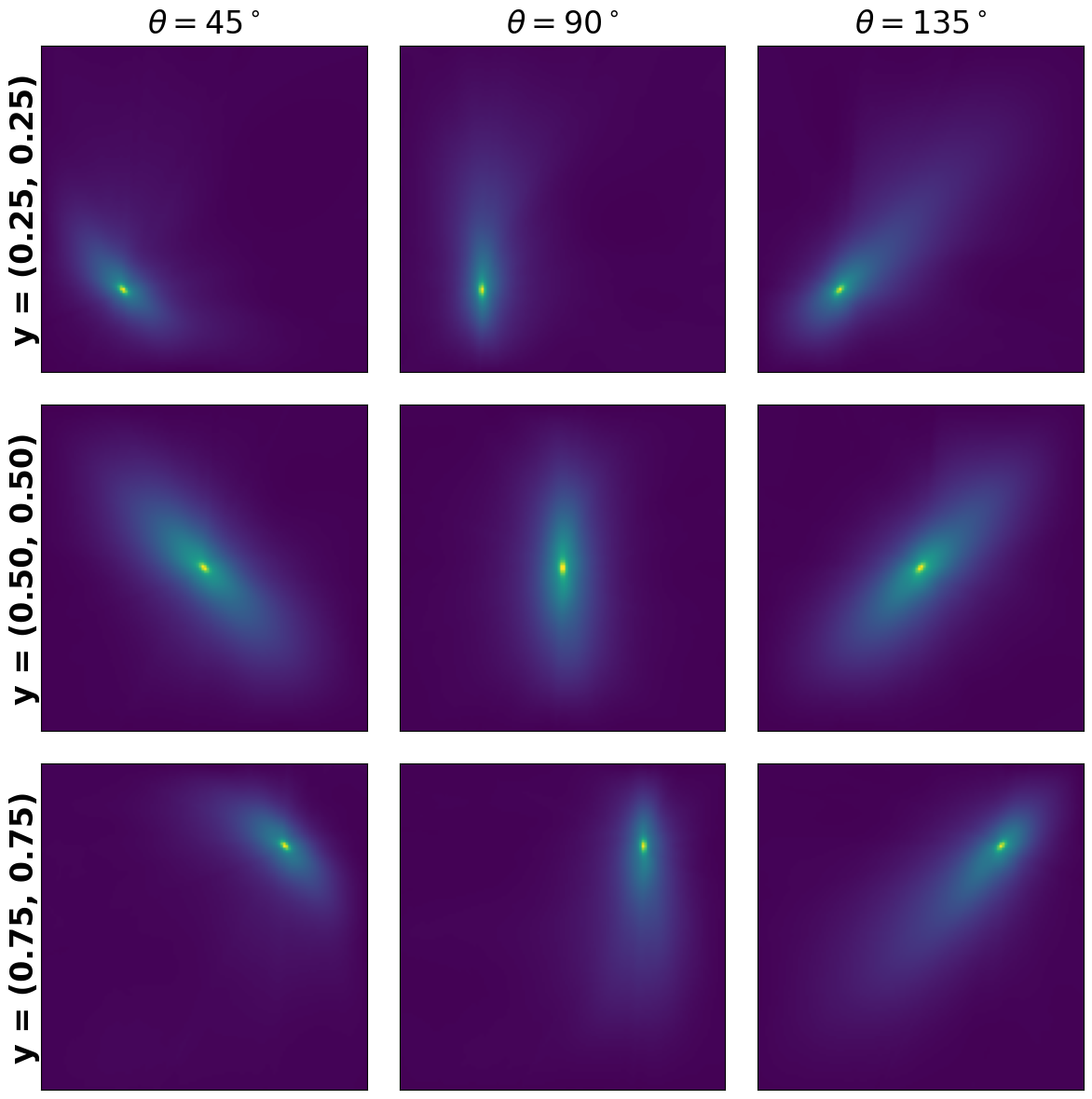
Embedding learning inside numerical solvers introduces large-scale, ill-conditioned optimization challenges, often under severe stochastic noise. I develop geometry-aware optimization methods, including preconditioned stochastic gradient descent and adapted Anderson acceleration. These techniques reshape the optimization landscape, enabling stable, fast convergence and significant variance reduction for complex scientific machine learning tasks.
Computation: Hardware-Efficient Scalability
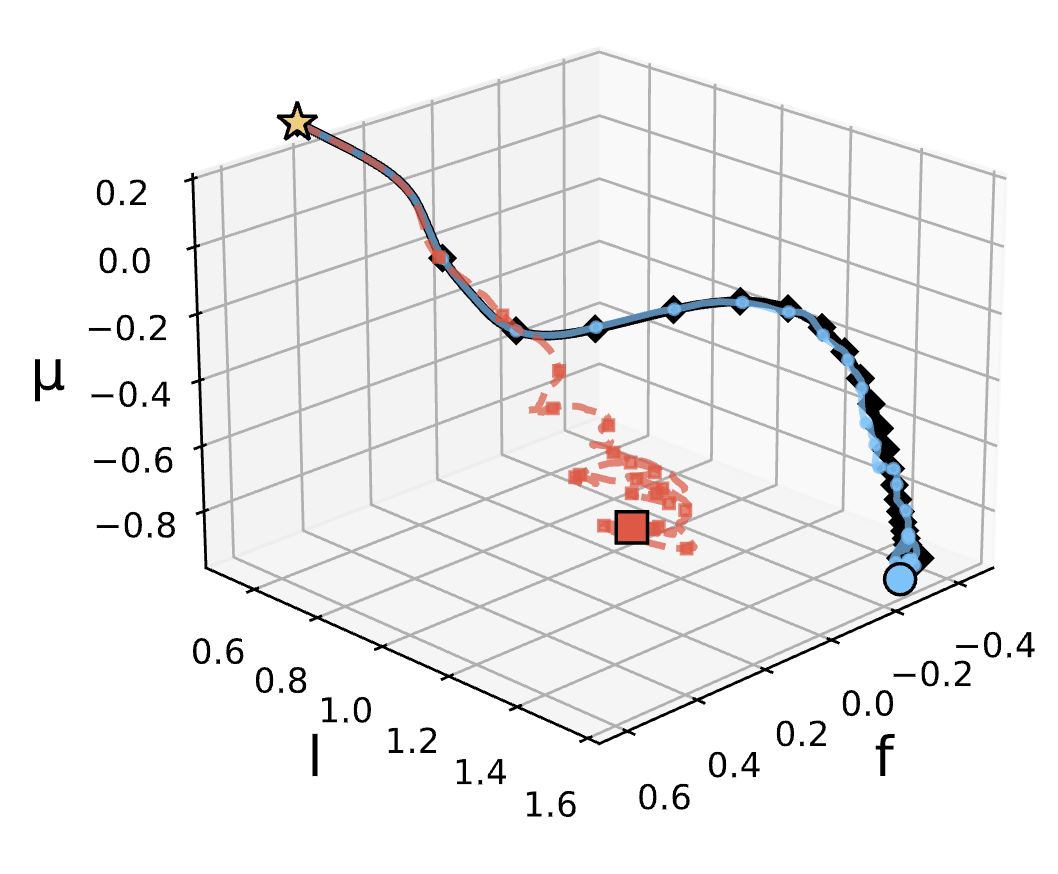
For mathematically accurate and convergent methods to be practically viable, they must map efficiently to modern hardware. I treat computational efficiency as a core algorithm design constraint. Through domain decomposition, memory-aware kernels, and mixed-precision linear algebra, I ensure these end-to-end solvers scale seamlessly on GPU-accelerated and distributed-memory systems.